Stoffwechsel-Modellierung & -Simulation
(Elektronentransportkette von Escherichia coli)
(Stand: Juni 2016)
Im Stoffwechsel (Metabolismus) reagieren Stoffwechselpartner (Metabolite) miteinander, ändern dadurch ihre Konzentration und bewirken bestimmte makroskopische Funktionen (beispielsweise Energiegewinnung oder Wachstum). Dabei erfüllen Proteine die Aufgabe als Enzyme, also als Katalysatoren von Reaktionen. Die Aktivität eines Enzyms, welche vor allem durch die Menge bzw. Konzentration gegeben ist, hat einen wesentlichen Einfluss auf die Geschwindigkeit einzelner Reaktionen sowie dadurch auch auf andere Reaktionen und letztendlich auf makroskopische Phänomene. Die Enzymmenge kann in Abhängigkeit geänderter Bedingungen mithilfe der Genexpression reguliert werden. Dadurch erreichen Lebewesen insgesamt eine Anpassung des Stoffwechsels.
Zur Beantwortung biologischer Fragestellungen zu Teilaspekten der Stoffwechsel unterschiedlicher Lebewesen wird die systembiologische Modellierung eingesetzt. In diesem Fall liegt der Fokus weniger auf dem Finden der Reaktionsstrukturen als vielmehr auf Mechanismen, ihren Parametern und insbesondere auf den Teilmodellen, die die Regulation beschreiben. Der Modellierung schließt sich in den meisten Fällen eine Identifikation der unbekannten Parameterwerte an; gefolgt von Simulationen und ihrer Auswertung. Im Folgenden wird anhand eines realitätsnahen Beispiels die Anwendung dieser einzelnen Schritte gezeigt.
Fragestellung
In den Reaktionen der Elektronentransportkette (ETK, auch: Atmungskette) werden Elektronen des zentralen Stoffwechsels auf Elektronenakzeptoren übertragen und gleichzeitig ein Protonenpotential geschaffen, welches schließlich zur Bildung des biochemischen Energieträgers ATP verwendet wird. Zur Anpassung an unterschiedliche Bedingungen werden die Reaktionen der ETK reguliert. Unterstützt durch ein kinetisches Modell wurde durch Henkel et al. die Anpassung des Bakteriums Escherichia coli an unterschiedliche Sauerstoffbedingungen untersucht:
[1] S. G. Henkel, A. Ter Beek, S. Steinsiek, S. Stagge, K. Bettenbrock, M. J. Teixeira de Mattos, T. Sauter, O. Sawodny, M. Ederer: "Basic regulatory principles of Escherichia coli's electron transport chain for varying oxygen conditions." In: PLoS ONE, 9(9):e107640, 2014. doi: 10.1371/journal.pone.0107640.
Dabei wurden ausschließlich stationäre Arbeitspunkte im Chemostat (kontinuierliche Kultivierung), siehe [2, 3], bei unterschiedlichen Sauerstoffbedingungen untersucht. Als wesentliche Grundlage für den biologischen und experimentellen Hintergrund sei außerdem auf [4–6] verwiesen. Die vorliegenden Messdaten zeigen ein charakteristisches Verhalten in bestimmten Komponenten (sowohl Metabolitkonzentrationen als auch eine Transkriptionsfaktor-Aktivität), welches den Ausgangspunkt für die kinetische Modellierung bildet. Im Folgenden soll in stark vereinfachter Form (und auf der Basis künstlicher Messdaten) nur ein Teilmodell der regulierten ETK hergeleitet werden (für die Formeln muss JavaScript aktiviert sein), während für eine ausführliche Beschreibung auf die genannte Publikation verwiesen wird. Es soll gezeigt werden, welche regulatorische Strukturen die Messdaten erklären können und ob dabei Ubichinon der wesentliche inhibierende Faktor für ArcA sein kann.
Modellierung
Den Ausgangspunkt der Modellierung bildet die folgende Abbildung der vergleichsweise verlässlichen strukturellen Information über die Reaktionen der ETK sowie die Existenz der zwei Transkriptionsfaktoren FNR und ArcA, deren regulatorische Wirkung im Rahmen der Modellierung analysiert werden soll (da die vorhandenen Informationen entweder weniger verlässlich oder widersprüchlich sind bzw. Messdaten nur unzureichend erklären):
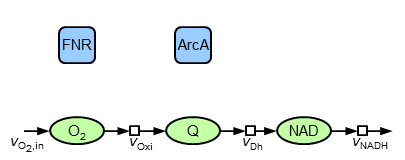
(Im Folgenden werden bei der Beschreibung nicht alle Annahmen begründet) Sauerstoff wird aufgenommen und reagiert in Reaktionen vom Oxidase-Typ. Dadurch wird Ubichinol (QH$_2$) zu Ubichinon (Q) oxidiert. Dieses Redoxpaar ist - wie auch NADH|NAD - außerdem an Dehydrogenase-Reaktionen beteiligt. Die verfügbaren Elektronen des zentralen Stoffwechsels werden durch NADH repräsentiert, wobei das Modell hier so entwickelt wurde, dass es aus den oxidativen Species aufgebaut ist, weshalb noch ein Abfluss von NAD benötigt wird ("Schnittstelle" zum zentralen Kohlenhydrat-Metabolismus). Als mathematisches Modell dieser Struktur werden folgende Differentialgleichungen aufgestellt:
\begin{align} {\dot c}_\mathrm{O_2} &= v_\mathrm{O_{2},in}-v_\mathrm{Oxi} \\ {\dot c}_\mathrm{Q} &= v_\mathrm{Oxi}-v_\mathrm{Dh} \\ {\dot c}_\mathrm{NAD} &= v_\mathrm{Dh}-v_\mathrm{NADH} \end{align}Es wird angenommen, dass erstens die Reaktionen quasi irreversibel sind, dass zweitens zusammengefasste Reaktionen der Isoenzyme verwendet werden können, weshalb im Folgenden nur noch von DER Oxidase und DER Dehydrogenase die Rede sein wird und dass drittens die Gesamtmenge an oxidativen und reduzierten Species konstant ist, also Q+QH$_2$=const. und NAD+NADH=const. Für die Ratengleichungen werden bekannte, das heißt physiologisch plausible, Kinetiken eingesetzt:
\begin{align} v_\mathrm{O_{2},in} &= \frac{v_\mathrm{O_{2},in,100\%}\times t}{t_\mathrm{end}}\\ v_\mathrm{Oxi} &= a_\mathrm{Oxi}\frac{c_\mathrm{O_{2}}}{(K_\mathrm{m,Oxi,O_{2}}+c_\mathrm{O_{2}})}\frac{c_\mathrm{QH_{2}}}{(K_\mathrm{m,Oxi,O_{2}}+c_\mathrm{QH_{2}})}\\ v_\mathrm{Dh} &= a_\mathrm{Dh}\frac{c_\mathrm{Q}}{(K_\mathrm{m,Dh,Q}+c_\mathrm{Q})}\frac{c_\mathrm{NADH}}{(K_\mathrm{m,Dh,NADH}+c_\mathrm{NADH})}\\ v_\mathrm{NADH} &= v_\mathrm{max,NADH}\frac{c_\mathrm{NAD}/c_\mathrm{NADH}}{K_\mathrm{m,NAD}+c_\mathrm{NAD}/c_\mathrm{NADH}} \end{align}Bei der Oxidase und Dehydrogenase sind die Enzymaktivitäten mit den Maximalgeschwindigkeiten gleichgesetzt. Über $v_\mathrm{O_{2},in}$ wird der Sauerstoff langsam verfahren, wodurch die resultierenden Simulationen mit den stationären(!) Messdaten vergleichbar werden. Nun ist die Frage, ob und wie in diesem Setting die folgenden Messdaten von Sauerstoff, Ubichinon und ArcA für verschiedene Sauerstoffbedingungen (anaerob...mikroaerob...aerob, repräsentiert durch prozentuale "Aerobiose" $a$, siehe [4–6]) erklärt werden können:
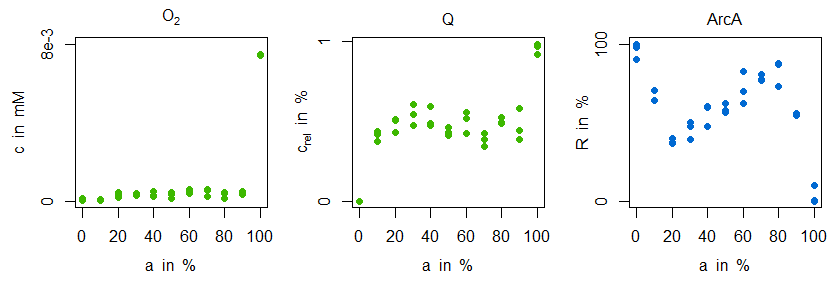
Im wesentlichen ist zu beobachten, dass sowohl Sauerstoff als auch Ubichinon im mikroaeroben Bereich ein nahezu konstantes Verhalten aufweisen (mit starken Anstiegen um 100% Aerobiosis), während ArcA einen charakteristischen "Zickzack"-Verlauf besitzt. Zur sensitiven Regulation ("Stabilisierung", "Homöostase") der Sauerstoffkonzentration wird folgende Teilstruktur eingeführt (es handelt sich aufgrund der beiden Inhibierungen um eine positive Regulation, jedoch bezüglich Sauerstoff aufgrund der Oxidasereaktion um eine negative Rückkopplung):
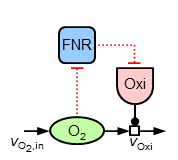
Für die beobachtete sensitive Regulation werden zu dieser Struktur noch folgende Gleichungen eingeführt:
\begin{align} R_\mathrm{FNR} &= \frac{c_\mathrm{O_{2}}^{n_\mathrm{FNR}}}{(K_\mathrm{A,FNR,O_{2}}^{n_\mathrm{FNR}}+c_\mathrm{O_{2}}^{n_\mathrm{FNR}})}\\ v_\mathrm{syn,Oxi} &= p_\mathrm{syn,Oxi,min} + p_\mathrm{syn,Oxi,FNR} \times (1-R_\mathrm{FNR})\\ {\dot a}_\mathrm{Oxi} &= v_\mathrm{syn,Oxi}-D \times a_\mathrm{Oxi} \end{align}
Mit der letzten Gleichung ist nun als weitere Variable eine veränderliche Enzymaktivität eingeführt worden, welche in der Oxidase-Ratengleichung die Funktion einer variablen Maximalaktivität erfüllt. Die Veränderung dieser Aktivität hängt von der Synthese und der "Verdünnung durch Wachstum" ab. Die Syntheserate $v_\mathrm{syn,Oxi}$ wiederum ist eine algebraische Gleichung, in welcher der erste Term eine grundlegende Expression repräsentiert und es einen zweiten Term gibt, welcher negativ vom Transkriptionsfaktor abhängt. Das entscheidende für eine sensitive Regulation ist nun die Gleichung für den Transkriptionsfaktor, da es sich um eine algebraische Gleichung ähnlich einer Hill-Kinetik handelt, bei welcher ein betraglich hoher negativer Exponent eine inhibierende sensitive Funktionalität gewährleistet (Randbemerkung: ähnlich zur Kooperativität kann auch hier ein solches Verhalten durch sequentielle Bindungen, mehrere Bindestellen und andere Effekte erklärt werden). Diese sensitive Regulation ist in der folgenden linken Abbildung gezeigt:
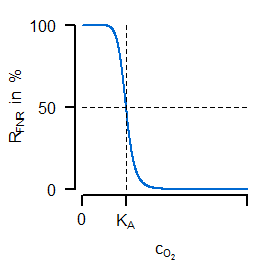
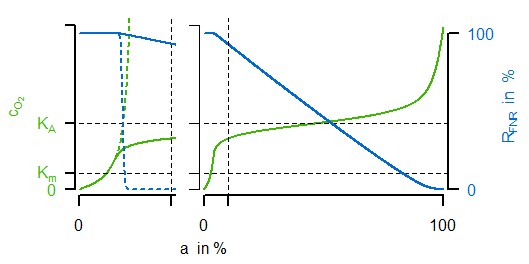
Dabei besitzt FNR eine sinkende Aktivität bei steigender Sauerstoffkonzentration mit einem quasi-schaltenden Verhalten um $K_A$ herum. In der rechten Abbildung ist nun der Vergleich der Simulationen für den unregulierten (gestrichelt) und regulierten (durchgezogen) Fall dargestellt. Es ist gut erkennbar, wie ein nahezu konstanter Verlauf der Sauerstoffkonzentration (grün, mit den entsprechneden charakteristischen Parametern der Enzymkinetik und Regulation) bei unterschiedlichem Sauerstoffeintrag in den Reaktor erreicht werden kann (nicht gezeigt: die resultierende, ansteigende Rate der Oxidasereaktion).
Nun stellt sich die Frage, ob und wie auf ähnliche Weise auch die Ubichinon-Konzentration und die ArcA-Aktivität erklärt werden kann. Dazu werden die folgenden zwei Varianten (im Folgenden "M1" und "M2") von Regulationsstrukturen analysiert:
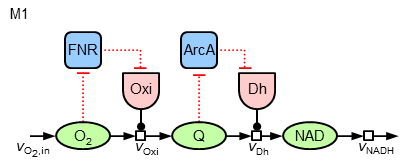
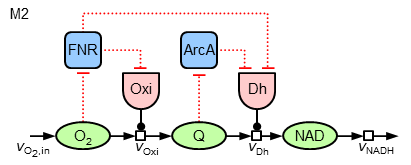
Die Gleichungen werden analog zur Regulation der Oxidase aufgestellt. Bei M2 kommt neben einer "lokalen" Regulation der Dehydrogenase durch ArcA noch eine vorsteuernde Regulation durch FNR hinzu (entsprechend ergeben sich dann drei additive Terme in der Synthesegleichung).
Da die Bestimmung unbekannter Parameterwerte mithilfe von Messdaten ein wesentlicher Schritt in der Stoffwechselmodellierung darstellt, wird dies im Folgenden anhand der Anpassung dieser beiden Varianten vorgestellt.
Parameteridentifikation
Bei der automatischen Bestimmung von Parametern mithilfe von Messdaten, also der Parameteridentifikation (oder Schätzung), werden die Parameter $\underline{\theta}$ so gefunden, dass die parameterabhängigen, simulierten Verläufe $\hat{y}_i$ der Variablen ihren gemessenen Werten so gut wie möglich entsprechen. Eine Simulation von Modellen, die durch gewöhnliche Differentialgleichungen beschrieben werden, erfolgt durch das automatische "Lösen eines Anfangswertproblems" mit entsprechenden Verfahren, die wiederum in diversen Computer-Umgebungen oder -Sprachen implementiert sind. Die Abweichung zwischen Simulation und Messung wird durch eine Zielfunktion (Gütefunktion, u.a.) beschrieben. Unter der Annahme normalverteilter Unsicherheiten der Messwerte (mit Varianzen $\sigma_{i}^2$) kann folgende Zielfunktion aufgestellt werden, bei der die Parameteridentifikation durch die Minimierung der Summe der Fehlerquadrate erreicht wird:
\begin{align} \chi^2(\underline{\theta}) &= \sum_{i=1}^{N}\frac{\left(y_{i}-\hat{y}_{i}(\underline{\theta})\right)^2}{\sigma_{i}^2} \end{align}
Die Minimierung erfolgt iterativ ebenfalls durch Implementierungen entsprechender (nichtlinearer) Optimierungsverfahren. Die identifizierten Parameterwerte der beiden Modellvarianten können der folgenden Tabelle entnommen werden:
| $K_\mathrm{m,Oxi,O_2}$ | $K_\mathrm{m,Oxi,QH_2}$ | $K_\mathrm{m,Dh,Q}$ | $K_\mathrm{m,Dh,NAD}$ | $v_\mathrm{max,NADH}$ | $K_\mathrm{m,NADH}$ | $K_\mathrm{A,FNR,O_2}$ | $n_\mathrm{FNR}$ | $K_\mathrm{A,ArcA,Q}$ | $n_\mathrm{ArcA}$ | $p_\mathrm{syn,Oxi,min}$ | $p_\mathrm{syn,Oxi,FNR}$ | $p_\mathrm{syn,Dh,min}$ | $p_\mathrm{syn,Dh,ArcA}$ | $p_\mathrm{syn,Dh,FNR}$ | |
| $\mathrm{M1}$ | $4.51\mathrm{e}{-5}$ | $1\mathrm{e}{-5}$ | $4.06\mathrm{e}{-3}$ | $1.56\mathrm{e}{-3}$ | $11.91$ | $6.12$ | $3.63\mathrm{e}{-4}$ | $-10$ | $0.52$ | $-10$ | $0.68$ | $1.68$ | $7.97\mathrm{e}{-3}$ | $4.32$ | $\mathrm{---}$ |
| $\mathrm{M2}$ | $9.42\mathrm{e}{-5}$ | $0.05$ | $0.01$ | $0.01$ | $12.00$ | $2.5$ | $4.02\mathrm{e}{-4}$ | $-10$ | $0.50$ | $-9.98$ | $0.74$ | $4.50$ | $0.01$ | $0.75$ | $4.8$ |
Es ist hervorzuheben, dass starke Unterschiede in den Parameterwerten der Regulation auftreten. Vor allem bei der Regulation der Dehydrogenase ist zu beobachten, dass einerseits bei Fehlen der Regulation durch FNR (M1) die ArcA-abhängige Regulation stärker ist als bei M2, bei welcher andererseits FNR den stärksten Einfluss auf die Regulation der Dehydrogenase ausübt.
Systembiologische Analyse und Interpretation
In der folgenden Abbildung werden die Simulationen der parameteridentifizierten Modellvariante M1 mit den Messdaten verglichen:
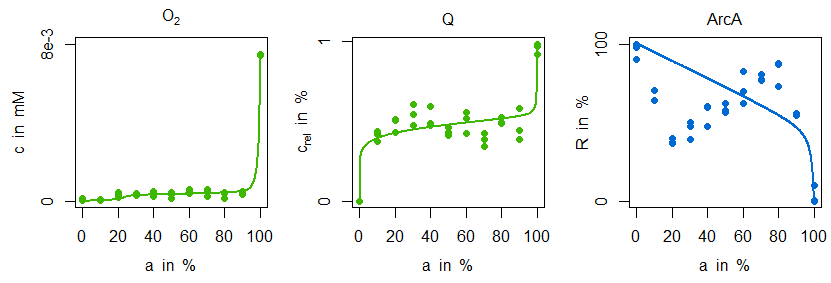
Es ist gut erkennbar, dass die sensitive Regulation tatsächlich auch eine vergleichsweise gute Anpassung für Ubichinon bedeutet. Es ist jedoch nicht möglich, den charakteristischen Verlauf der ArcA-Messdaten zu erklären. Anders sieht es da bei der angepassten Modellvariante M2 aus. Hier wird nicht nur der ArcA-Verlauf gut getroffen, sondern auch der zuvor kaum erkennbare schwache Abfall von Ubichinon im mikroaeroben Bereich gut wiedergegeben:
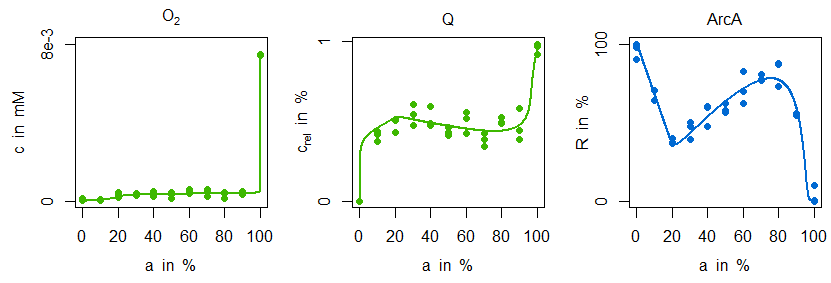
Dieses Verhalten wird letztendlich durch den zusätzlichen regulatorischen Einfluss von FNR auf die Dehydrogenase erklärbar: die Information über eine gesteigerte Sauerstoffverfügbarkeit wirkt sich überproportional auf diese Enzymaktivität aus, wodurch der leichte Ubichinonabfall im oberen mikroaeroben Bereich einen Anstieg von ArcA mit sich bringt. Aus biologischer Sicht hat das zum einen den Vorteil, mit dem Transkriptionsfaktor ArcA eine differenziertere Regulation für andere Stoffwechselwege und Isoenzyme zu erreichen, und zum anderen besitzt dieses regulatorische Motiv bessere Eigenschaften bei dynamischen Änderungen, [7], hier also bei schnelleren Schwankungen der Sauerstoffverfügbarkeit.
In der oben genannten Publikation wurden die hier beschriebenen Prinzipien der regulierten ETK innerhalb eines umfangreicheren Modells (u.a. mit phämomenologischem Biomassemodell) angewendet und diskutiert.
Referenzen
- [1] S. G. Henkel, A. Ter Beek, S. Steinsiek, S. Stagge, K. Bettenbrock, M. J. Teixeira de Mattos, T. Sauter, O. Sawodny, M. Ederer: Basic regulatory principles of Escherichia coli's electron transport chain for varying oxygen conditions. In: PLoS ONE, 9(9):e107640, 2014. doi: 10.1371/journal.pone.0107640
- [2] A. Novick, L. Szilard: Experiments with the Chemostat on spontaneous mutations of bacteria. In: Proc. Natl. Acad. Sci. USA, 36(12):708–719, 1950. doi: 10.1073/pnas.36.12.708
- [3] A. Novick, L. Szilard: Description of the Chemostat. In: Science, 112:715–716, 1950. doi: 10.1126/science.112.2920.715
- [4] S. Alexeeva, B. de Kort, G. Sawers, K. J. Hellingwerf, M. J. Teixeira de Mattos: Effects of limited aeration and of the ArcAB system on intermediary pyruvate catabolism in Escherichia coli. In: J. Bacteriol., 182(17):4934–4940, 2000. doi: 10.1128/JB.182.17.4934-4940.2000
- [5] S. Alexeeva, K. J. Hellingwerf, M. J. Teixeira de Mattos: Quantitative assessment of oxygen availability: perceived aerobiosis and its effect on flux distribution in the respiratory chain of Escherichia coli. In: J. Bacteriol., 184(5):1402–1406, 2002. doi: 10.1128/JB.184.5.1402-1406.2002
- [6] S. Alexeeva, K. J. Hellingwerf, M. J. Teixeira de Mattos: Requirement of ArcA for redox regulation in Escherichia coli under microaerobic but not anaerobic or aerobic conditions. In: J. Bacteriol., 185(1):204–209, 2003. doi: 10.1128/JB.185.1.204-209.2003
- [7] S. Mangan, U. Alon: Structure and function of the feed-forward loop network motif. In: Proc. Natl. Acad. Sci. USA, 100(21):11980–11985, 2003. doi: 10.1073/pnas.2133841100
